재귀함수
하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘
재귀는 문제를 작은 부분으로 나누어 해결하는 방식에 효과적으로 적용 가능!
- 함수가 자기 자신을 호출하여 문제를 해결하는 방법
- 기본 조건과 재귀 호출로 구성
- 문제를 반복적으로 나누어 해결하는 반복적인 호출 방법으로 효율성에 초점을 두지 않음
- 단순 반복적 문제인 피보나치 수열, 팩토리얼 계산 등 적용
0~N까지의 합 코드
package org.example;
public class N의합 {
public static void main(String[] args) {
System.out.println(rec(10));
}
public static int rec(int n){
if(n == 0) return 0;
return rec(n-1) +n;
}
}
구성요소
기저 조건(Base Case) - 재귀함수를 끝낼 수 있는 조건
재귀호출 (Recursive Call)
재귀함수 문제
특정 입력에 대해서는 자기 가신을 호출하지 않고 종료되어야 함(Base Case)
모든 입력은 Base Case로 수렴
*런타임에러 주의
- 거듭제곱 문제
- 팩토리얼 계산
5! = 5*4*3*2*1
// 함수의 호출은 Stack에 순서대로 쌓이며 가장 최근에 호풀된 함수부터 실행
public static int fac(int n){
if(n <=1) return 1;
return n* fac(n -1);
}
fac(5);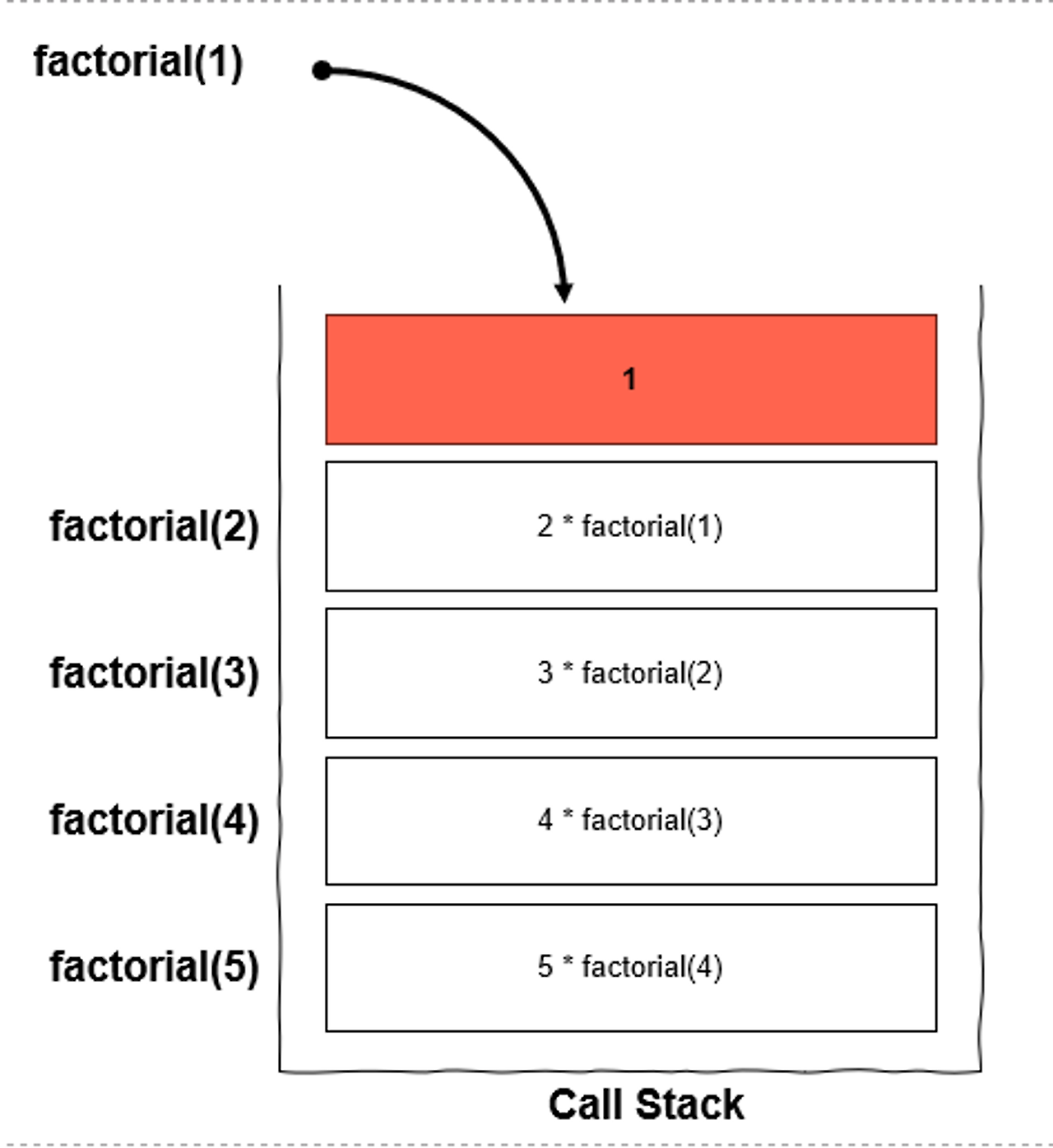
- 피보나치 수열 계산
// 앞전의 두 수를 가지고와 더해서 지금의 숫자를 만든다!
f(n) = f(n-1) + f(n-2)
재귀함수 스택오버플로
재귀함수 사용에는 스택 오버플로우(Stack overflow)를 주의 해야한다!
public static int fac(int n){
return n* fac(n -1);
}해당 코드와 같이 Base Case가 없다면 함수가 멈추지 않고 무한 반복되고 스택 오버플로우를 발생시킨다.
재귀 함수의 장단점
장점
변수를 여러개 만들 필요가 없다. 코드도 간결해 진다
단점
지속적으로 함수를 호출하게 되면 지역변수, 매개변수, 반환값을 모두 Stack에 저장해야한다. 메모리를 더 많이 사용하게 되고, 속도 저하로 이루어진다.
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| [알고리즘] 투포인터 (0) | 2024.07.18 |
|---|---|
| [알고리즘] 정렬 (1) | 2024.05.09 |
| [알고리즘] BFS(Breadth-First Search) - 너비우선탐색 (0) | 2024.05.09 |
| [알고리즘] DFS(Depth-First Search) - 깊이우선탐색 (0) | 2024.05.07 |
| [알고리즘] 스택(Stack) / 큐(Queue) / 데크(Deque) (0) | 2024.05.06 |