재귀함수로 문제를 풀던중 너무 큰 값이 들어갔을 때 스택 오버플로우가 발생했다
재귀 방식과 유사한 DP방식을 알아볼까한다!
중복되는 하위 문제와 최적 부분 구조를 활용하여 문제를 해결
동적 계획법(DP : Dynamic programming)이란?
하나의 큰 문제를 여러 개의 작은 문제로 나누고, 같은 문제라면 한 번씩만 풀어 그 결과를 저장해서 다시 큰 문제를 해결할 때 사용) 효율적으로 해결하는 알고리즘
DP사용 방법
모든 작은 문제들을한 번만! 풀어야 하는 게 point!
정답을 구한 작은 문제를 어딘가에 메모해두어야 함
다시 그 보다 큰 문제를 풀어갈 때 똑같은 작은 문제가 나타나면 앞서 메모한 작은 문제의 결과 값을 다시 사용
DP 구성
- 문제분할 : 하나의문제를 작은 하위 문제로 나누어 해결
- 중복계산 방지 : 이전 계싼 결과를 저장하여 동일한 계산을 반복하지 않음
- 최적 부분 구조 : 문제의 최적 해가 하위 문제의 최적해로구성될 수 있는 구조
DP 사용 조건
- 작은 문제가 반복이 일어나는 경우
- 같은 문제는 구할 때마다 정답이 같아야 함
Memoization 기법
DP를 구현하는 방법 중 한 종류
한번 구한 결과를 메모리 공간에 메모해 두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법
메모이제이션은 값을 저장하는 방법으로 캐싱(Caching)이라고도 함
예시 : 피보나치
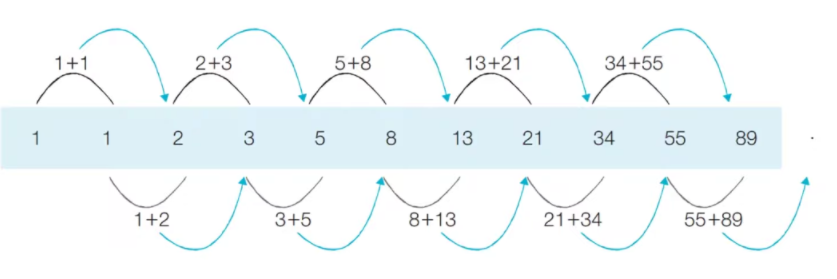
수학적 점화식을 프로그래밍으로 표현해 보면
public static int fibo(int x) {
if (x == 1 || x == 2) {
return 1;
}else{
fibo(x -1) + fib(x - 2);
}
}
재귀를 이용
- 함수를 반복 호출 하게 되면서 수행시간이 기하급수적으로 늘어남!
- 숫자가 커질수록 시간이 오래 걸리게 됨
- 사간 복잡도 :

DP를 이용
- 색칠한 노드만 방문하면 되기 때문에 재귀보다 시간이 작음
- 시간 복잡도 : O(n)

DP 문제 푸는 방법
탑다운(Top-Down) - 하향
- 큰 문제를 해결하기 위해 작은 문제를 호출하는 방법 - 재귀적으로 호출
- 메모이제이션 방법을 통해 중복 계산을 피함
- 점화식을 이해하기 쉬운 장점이 있다.
public class Fibonacci {
private static int[] memo;
public static int fib(int n) {
if (n <= 1) return n;
if (memo[n] != 0) return memo[n];
memo[n] = fib(n - 1) + fib(n - 2);
return memo[n];
}
public static void main(String[] args) {
int n = 10;
memo = new int[n + 1];
System.out.println(fib(n)); // 55
}
}
보텀업(Bottom-Up) -상향식
- 하위 문제를 해결하고 그결과를 이용해 상위 문제 해결
- 단순히 반복문을 이용하여 소스 코드를 작성 , 타뷸레이션(Tabulation)이라고 함
- 재귀 호출을 하지 않기 때문에 시간과 메모리 사용량을 줄일 수 있는 장점이 있다.
- 결과 저장용 리스트는 'DP테이블'이라고 부름
public class Fibonacci {
public static int fib(int n) {
if (n <= 1) return n;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
public static void main(String[] args) {
int n = 10;
System.out.println(fib(n)); // 55
}
}
1. 테이블 정의 하기
2. 점화식 찾기
3. 초기값 정의하기
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| [알고리즘] 힙 / 해시 테이블 (0) | 2024.07.24 |
|---|---|
| [알고리즘] 백트래킹 (0) | 2024.07.23 |
| [알고리즘] 투포인터 (0) | 2024.07.18 |
| [알고리즘] 정렬 (1) | 2024.05.09 |
| [알고리즘] 재귀함수 (0) | 2024.05.09 |