백트래킹
현재상태에서 가능한 모든 후보군을 따라 들어가며 탐색하는 알고리즘
어떤 노드의 '유망성'을 판단한뒤, 해당 노드가 유망라지 않으면 부모 노드로 돌아가 다른 자식 노드를 찾는 방법
즉, 모든 경우의 수를 찾아보지만, 그 중에서도 가능성만 있는 경우의 수만 찾아보는 방법
- 가능한 모든해를 탐색하면서 유효하지 않은 해가 나오면 되돌아가 다른 해를 찾음
- 재귀를 사용하며, 가지치기(Plunning)을 통해 효율성을 높임
- 해 공간이 매우 커서 전체 탐색이 어려운 탐색문제, 최적화 문제, 제약조건 문제 등에 적용
간혹, 브루트포스와 백트래킹, dfs를 혼동하는 경우가 있다.
브루트포스는 '모든 경우의 수' 를 찾아보는것
장점은 모든 경우의 수를 탐색하다보니 만족값을 100%찾아낸다
하지만 단점은 모든 경우의 수를 판단하는 만큼 경우의수가 많아지면 많은 자원을 필요로 한다
DFS은 트리 순회의 한 형태이다. 하나의 순회 알고리즘으로 백트래킹에서 사용하는 대표적인 탐색 알고리즘이다.
백트래킹 == DFS가 아니라 백트래킹의 방법 중 하나가 DFS인 것
외에도 BFS(너비우선탐색)등 다양한 방법으로 백트래킹을 구현할수 있다.
DFS는 말 그대로 깊이를 우선으로 탐색하는 방법이다
순열
N개의 수중 M개를 뽑아 나올수 있는 경우의수
DFS트리와 체크리스트 사용
DFS -> 반드시 종료 조건이 있어야함 / 모든 경우의 수를 찾을때
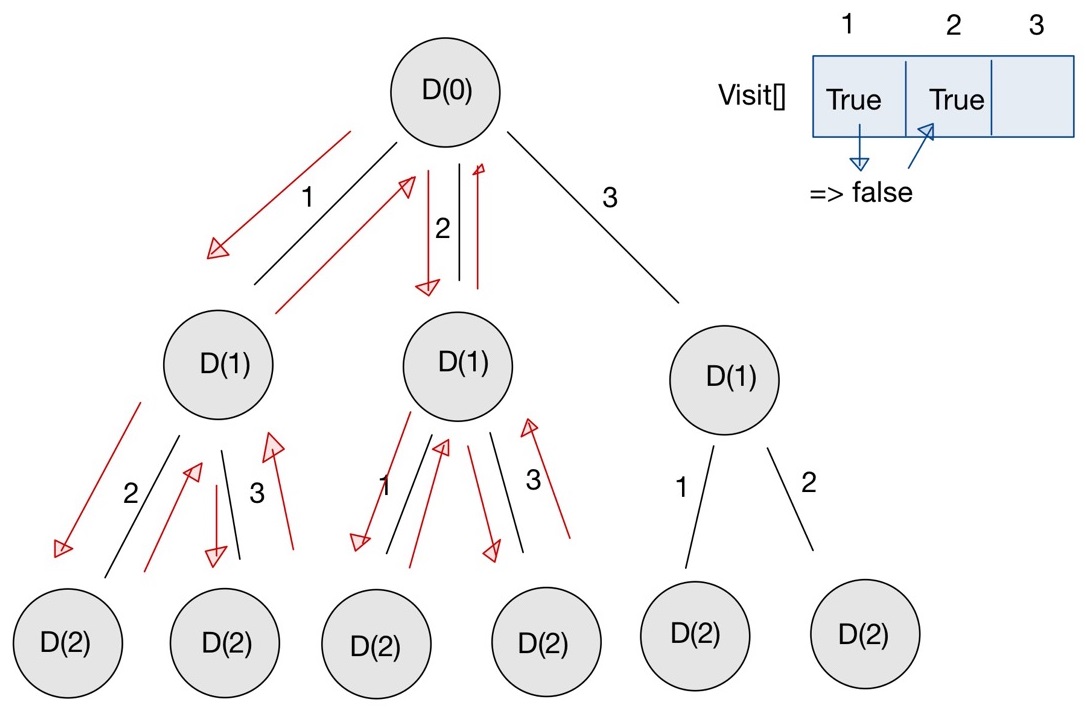
static int N = 3; // => 1,2,3 중
static int M = 2; // => 중복되지 않는 숫자 2개의 경우의수
static boolean[] visit;
static int[] arr;
public static void main(String[] args) throws IOException {
//방문 체크리스트 배열
visit = new boolean[N];
// 숫자를 담을 배열
arr = new int[M];
//depth를 시작할때는 0부터
dfs(N,M,0);
}
// dfs 함수 작성
// 작성시 주의할점 => 반드시 종료 조건이 있어야함
// 종료 조건 : depth = M;
public static void dfs (int N, int M, int depth){
//종료 조건 작성
if(depth == M){
// 마지막에 전부 출력
for(int val : arr){
System.out.print(val + " ");
}
System.out.println();
return;
}
for(int i = 0;i < N;i++){
if (!visit[i]) { // 방문하지 않은 숫자만 사용
visit[i] = true;
// 배열 채우기 1~N 까지의 숫자 넣기
arr[depth] = i + 1;
dfs(N, M, depth + 1);
visit[i] = false;
}
}
}
주의점!
백트래킹에서는 재귀의 방법으로 사용되기때문에 반드시 종료 조건이 있어야함
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| [알고리즘] 그래프와 트리 (0) | 2024.08.01 |
|---|---|
| [알고리즘] 힙 / 해시 테이블 (0) | 2024.07.24 |
| [알고리즘] 동적 계획법(DP : Dynamic programming) (0) | 2024.07.19 |
| [알고리즘] 투포인터 (0) | 2024.07.18 |
| [알고리즘] 정렬 (1) | 2024.05.09 |